1.95 Completed Pass. At Enormous State University (ESU), the football team records its plays using vector displacements, with the origin taken to be the position of the ball before the play starts. In a certain pass play, the receiver starts at $+1.0\hat{i} - 5.0\hat{j}$, where the units are yards, $\hat{i}$ is to the right, and $\hat{j}$ is downfield. Subsequent displacements of the receiver are $+9.0\hat{i}$ (in motion before the snap), $+11.0\hat{j}$ (breaks downfield), $-6.0\hat{i} + 4.0\hat{j}$(zigs), and $+12.0\hat{i} + 18.0\hat{j}$ (zags). Meanwhile, the quarterback has dropped straight back to a position $-7.0\hat{j}$. How far and in which direction must the quarterback throw the ball? (Like the coach, you will be well advised to diagram the situation before solving it numerically.)
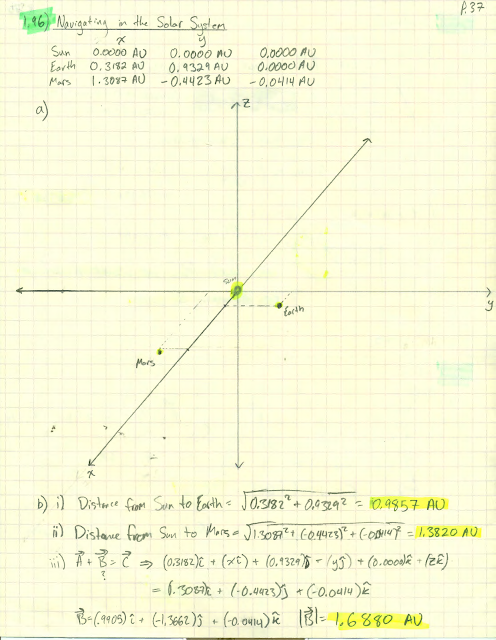
1.96 Navigating in the Solar System. The Mars Polar Lander spacecraft was launched on January 3, 1999. On December 3, 1999, the day that the Mars Polar Lander touched down on the Martian surface, the positions of the earth and Mars were given by these coordinates.
| x | y | z | |
| Earth | 0.3182 AU | 0.9329 AU | 0.0000 AU |
| Mars | 1.3087 AU | -0.4423 AU | -0.0414 AU |
In these coordinates, the sun is at the origin and the plane of the earth's orbit is the xy-plane. The earth passes through the +x-axis once a year on the autumnal equinox, the first day of autumn in the northern hemisphere (on or about September 22). One AU, or astronomical unit, is equal to $1.496 \times 10^8 km$, the average distance from the earth to the sun. a) In a diagram, show the positions of the sun, the earth, and Mars on December 3rd, 1999. b) Find the following distances in AU on December 3, 1999: i) from the sun to the earth; ii) from the sun to Mars; iii) from the earth to Mars. c) As seen from the earth, what was the angle between e direction to the sun and the direction to Mars on December 3, 1999? d) Explain whether Mars was visible from your location at midnight on December 3, 1999. (When it is midnight at your location, the sun is on the opposite side of the earth from you.)
1.97 Navigating in the Big Dipper. All the stars of the Big Dipper (part of the constellation Ursa Major) may appear to be the same distance from the earth, but in fact they are very far from each other. Figure 1.36 shows the distances from the earth to each of these stars. The distances are given in light years (ly), the distance that light travels in 1 year. One light year equals $9.461 \times 10^15 m$. a) Alkaid and Merak are $25.6^\circ$ apart in the earth's sky. In a diagram, show the relative positions of Alkaid, Merak, and our sun. Find the distance in light years from Alkaid to Merak. b) To an inhabitant of a planet orbiting Merak, how many degrees apart in the sky would Alkaid and our sun be?
1.98 The vector $\vec{r} = x\hat{i} + y\hat{j} + z\hat{k}$, called the position vector, which points from the origin (0, 0, 0) to an arbitrary point in space with coordinates (x, y, z). Use what you know about vectors to prove the following: All points (x, y, z) that satisfy the equation $Ax + By + Cz = 0$, where A, B, and C are constants, lie in a plane tat passes through the origin and that is perpendicular to the vector $A\hat{i} + B\hat{j} + C\hat{k}$. Sketch this vector and the plane.